Double Machine Learning

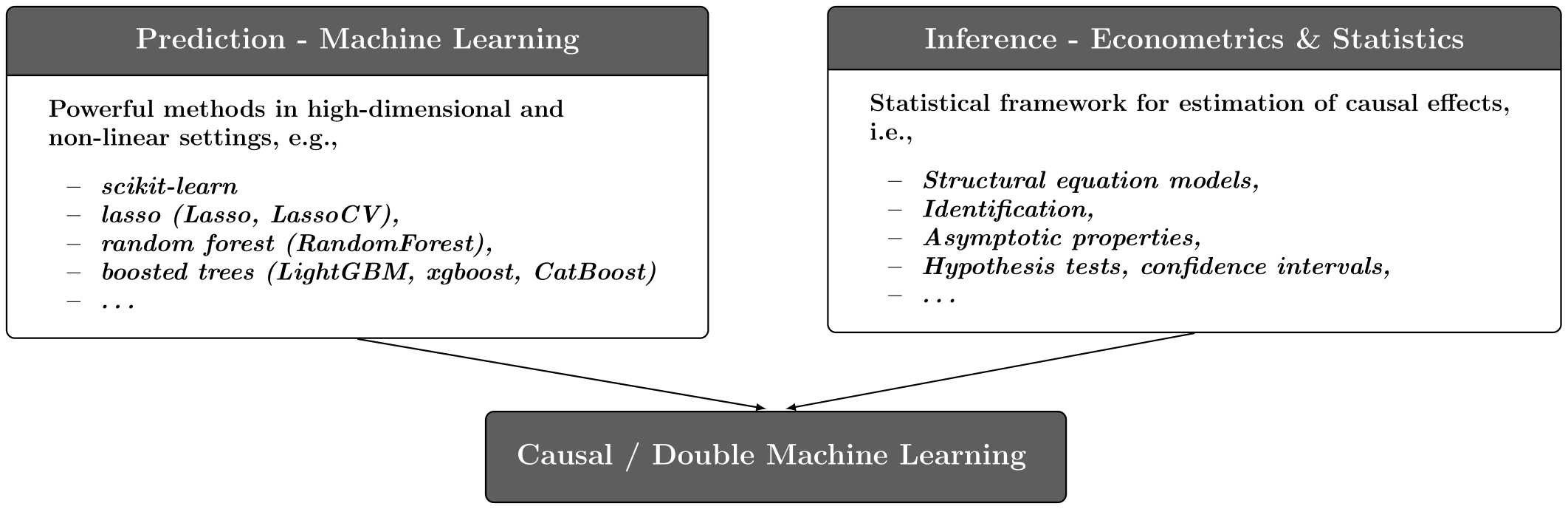
Double ML: Causal Inference based on ML

O Double Machine Learning (DML) representa uma metodologia moderna, situando-se na interseção entre a econometria e o Machine Learning (ML).

Para entendermos DML, vamos revisitar o Teorema de Frisch-Waugh-Lovell (FWL). Na regressão linear clássica, o FWL nos diz que podemos estimar o efeito de um tratamento $D$ sobre o outcome $Y$ em duas etapas:

"Limpando" $Y$ das covariáveis $X$ (pegando os resíduos).
"Limpando" $D$ das covariáveis $X$ (pegando os resíduos).
Regredindo os resíduos de $Y$ contra os resíduos de $D$ .

O DML generaliza essa ideia. Em vez de usar regressão linear para "limpar" os dados, usamos modelos de ML.

Artigos Sobre

Uplift Modeling Notebook
Demand Elasticity Notebook

Por que não usar apenas ML direto?

"Por que não apenas jogar $Y$ , $D$ e $X$ em um XGBoost e olhar o feature importance ou SHAP?"

O problema reside no Viés de Regularização. Modelos de ML são desenhados para prever bem, não para estimar parâmetros. Eles usam regularização (Lasso, profundidade de árvore, dropout) para evitar overfitting.

Ao fazer isso, eles "encolhem" os coeficientes das variáveis de confusão.
Esse viés na estimativa de $g (X)$ contamina a estimativa do efeito de tratamento $θ$ .

O DML resolve isso através da Ortogonalização, separando a etapa de previsão (ML) da etapa de inferência.

Os 4 Pilares

Framework Não-Paramétrico: Flexibilidade total para usar Random Forests, Gradient Boosting ou Redes Neurais para modelar as variáveis de controle ( $X$ ), capturando não-linearidades complexas automaticamente.
Redução de Viés: Resolve o viés de regularização mencionado acima, garantindo que o erro de predição do modelo de ML não interfira no coeficiente de tratamento.
Inferência Estatística Válida: É matematicamente difícil calcular p-valores de uma "caixa preta". O DML transforma o problema final em uma regressão linear simples sobre resíduos, recuperando a capacidade de calcular intervalos de confiança e significância clássicos ( $\sqrt{n}$ -consistent).
Eficiência Estatística: O estimador converge rapidamente à medida que a amostra $n$ cresce, comportando-se tão bem quanto uma regressão linear paramétrica, mesmo usando ML complexo "por trás das cortinas".

Algoritmos

Regressão Parcialmente Linear (PLR)

Assumimos um processo gerador de dados onde o efeito de $D$ é linear e aditivo, mas as confusas ( $X$ ) são complexas:

Y = \underset{Linear}{\underset{⏟}{D θ}} + \underset{Não-Linear}{\underset{⏟}{g (X)}} + U

D = m (X) + V

Onde $θ$ é o efeito causal, $g (X)$ é a função de confusão do outcome e $m (X)$ é a função do tratamento.

O Processo de Ortogonalização

Estimar Outcome ( $Y$ ): Usamos um modelo de ML para estimar $E [Y | X]$ (chamaremos de $l (X)$ ) e calculamos o resíduo:
$\tilde{Y} = Y - \hat{l} (X)$
Estimar Tratamento ( $D$ ): Usamos outro modelo de ML para estimar $m (X)$ (similar a um Propensity Score) e calculamos o resíduo:
$\tilde{D} = D - \hat{m} (X)$
Regressão Final: Uma regressão linear simples (OLS) dos resíduos:
$\tilde{Y} = θ \tilde{D} + ϵ$

Intuição dos Resíduos

Ao usarmos $\tilde{Y}$ e $\tilde{D}$ , estamos trabalhando apenas com a variação que não é explicada por $X$ . Isso isola a relação exógena entre $D$ e $Y$ .

Por que "Parcialmente Linear"?

O nome vem da estrutura da equação principal ( $Y = D θ + g (X) + U$ ). Ela é híbrida: possui um componente paramétrico linear ( $D θ$ ) para o tratamento, que queremos interpretar, e um componente não-paramétrico ( $g (X)$ ) para as covariáveis, que queremos apenas controlar flexivelmente.

Modelo de Regressão Interativa (IRM)

Enquanto a PLR assume que o tratamento apenas desloca o resultado de forma constante (aditiva), o IRM assume que o efeito do tratamento depende das características do indivíduo. Focamos aqui em tratamentos binários ( $D \in {0, 1}$ ).

Y = \underset{Baseline}{\underset{⏟}{g_{0} (X)}} + D \cdot \underset{Efeito Variável τ (X)}{\underset{⏟}{(g_{1} (X) - g_{0} (X))}} + U

D = m (X) + V

Onde:

$g_{0} (X) = E [Y | X, D = 0]$ : O outcome esperado para o grupo de controle.
$g_{1} (X) = E [Y | X, D = 1]$ : O outcome esperado para o grupo tratado.
$τ (X)$ : O Efeito Causal Condicional (CATE), que varia conforme $X$ .
$m (X)$ : A probabilidade de tratamento (Propensity Score).

O Processo de Estimação (AIPW)

Diferente da PLR que usa uma regressão única nos resíduos, o IRM utiliza a estrutura de Augmented Inverse Probability Weighting (AIPW) para garantir robustez.

Estimar os Potenciais Outcomes ( $g_{0}, g_{1}$ ): Treinamos modelos de ML separados para aprender a curva de $Y$ nos tratados e nos não-tratados.
Estimar o Tratamento ( $m$ ): Treinamos um classificador de ML para prever a probabilidade de receber o tratamento (Propensity Score).
Combinação Duplamente Robusta: O algoritmo combina essas previsões para criar um "score" pseudo-outcome para cada indivíduo, que é então projetado nas variáveis $X$ ou agregado para obter o ATE.

ψ (W) = g_{1} (X) - g_{0} (X) + \frac{D (Y - g_{1} (X))}{m (X)} - \frac{(1 - D) (Y - g_{0} (X))}{1 - m (X)}

A Propriedade de Dupla Robustez

O estimador AIPW possui a mesma propriedade descrita sobre Estimador Duplamente Robusto: para ele convergir para o valor correto, apenas um dos dois modelos precisa estar bem especificado.

Se o modelo de propensity $m (X)$ for preciso (mesmo que $g (X)$ seja ruim), o estimador funciona.
Se o modelo de outcome $g (X)$ for preciso (mesmo que $m (X)$ seja ruim), o estimador funciona.

Por que "Interativo"?

O nome vem do termo de interação na equação estrutural. Na PLR, as curvas de $Y (0)$ e $Y (1)$ são paralelas (efeito fixo). No IRM, permitimos que as variáveis $X$ interajam com $D$ . Isso significa que as curvas podem ter inclinações diferentes, se cruzar ou divergir, permitindo identificar para quem o tratamento funciona (CATE) e para quem não funciona.

Premissas Importantes

É fundamental refrisar que esse método não é "bala de prata". A validade causal ainda depende das premissas anteriores:

Ignorabilidade: $Y (d) ⊥ D | X$ . Ou seja, todas as variáveis de confusão relevantes foram incluídas em $X$ . É importante refrisarmos isso que é assumido que foi capturando todos os confounders relevantes. Na prática, não temos como saber por exato, mas uma boa construção é importante.
Domínio sob regra de negócio: Para toda a inferência causal, aqui não muda. Por mais complexo que nosso modelo possa ser, ele sempre será limitado relativo a tomada de decisão às escolhas de variáveis. Um bom DAG construído ainda é necessário, para evitar qualquer viés sob o resultado.
Qualidade de dados: por mais que o DoubleML é focado para estudos observacionais, aonde não controlamos variáveis de confusão e não temos uma randomização controlada, ele ainda pode sofrer com dados ruins. Se a extração tiver algum viés forte, problemas com campos, o resultado dele vai ser ineficiente para estimar causalidade.
Positividade: Para valores de $X$ relevantes, deve haver variação no tratamento (a probabilidade de tratamento $P (D | X)$ não deve ser nem 0 nem 1 estritos, como também valores extremos).
Regularidade: Os estimadores de ML devem convergir suficientemente rápido. O uso de Cross-Fitting é crucial para evitar viés de overfitting e garantir a validade assintótica.

O Perigo no Overfitting

Mesmo com a ortogonalização, se o modelo de ML decorar os dados (overfitting), os resíduos serão artificialmente pequenos, enviesando o $θ$ , eliminando a variação necessária para encontrarmos o efeito causal.

Por conta disso, a prática padrão é utilizar o Cross-Fitting:

Selecionamos $K$ possíveis folds.
No $K 1$ , separamos os dados por exemplo em "Treino" e "Hold-out".
O modelo é treinado apenas na base de Treino, e utilizamos os dados para calcular o resíduo do Hold-Out.
Agora, retreinamos o modelo com outro $K$ fold, até que todos os dados tenham seus resíduos calculados.

Assim, mesmo que o modelo aprenda nos dados de treino, ele não terá "visto" os dados de hold-out. Isso garante que os resíduos mantenham um ruído real e a variabilidade honesta necessária.

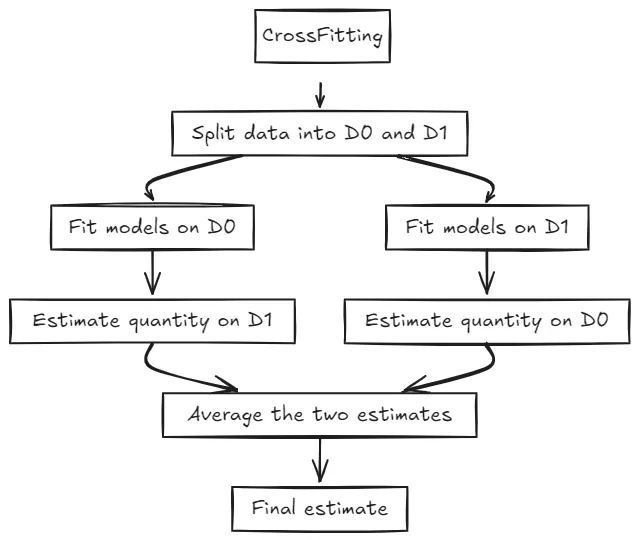
Double Machine Learning for Causal Inference: A Practical Guide | by Mohamed Hmamouch | Medium

Implementação Prática: Calculando ATE e CATE com Python

Vamos utilizar a biblioteca DoubleML para aplicar os conceitos acima.

1. Calculando o ATE

Para o ATE, assumimos um efeito constante e usamos o modelo PLR.

import numpy as np
import pandas as pd
from doubleml import DoubleMLData, DoubleMLPLR
from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier

# --- Configuração dos Dados ---
# Suponha que temos um DataFrame 'df' com:
# 'y': Outcome, 'd': Tratamento binário, 'X1'...'X5': Covariáveis
data_dml = DoubleMLData(df,
                        y_col='y',
                        d_cols='d',
                        x_cols=[f'X{i}' for i in range(5)])

# --- Definindo os Modelos (Learners) ---
# Modelo para prever Y (Outcome)
ml_l = RandomForestRegressor(n_estimators=100, max_depth=5)
# Modelo para prever D (Propensity Score)
ml_m = RandomForestClassifier(n_estimators=100, max_depth=5)

# --- Estimando ATE com Cross-Fitting ---
dml_plr = DoubleMLPLR(data_dml,
                      ml_l=ml_l,
                      ml_m=ml_m,
                      n_folds=3) # 3-fold Cross-Fitting

dml_plr.fit()
print(dml_plr.summary)

O resultado coef no sumário será o nosso $τ$ (ATE), livre do viés das covariáveis.

2. Calculando o CATE

Se quisermos saber como o efeito varia de acordo com as características da pessoa ( $X$ ), usamos o Interactive Regression Model (IRM). Em vez de calcular um número único, projetamos o efeito causal nas covariáveis usando um Preditor Linear.

from doubleml import DoubleMLIRM

# --- Usando IRM para permitir interações ---
# ml_g prevê E[Y|X, D] e ml_m prevê E[D|X]
ml_g = RandomForestRegressor(n_estimators=100, max_depth=5)
ml_m = RandomForestClassifier(n_estimators=100, max_depth=5)

dml_irm = DoubleMLIRM(data_dml,
                      ml_g=ml_g,
                      ml_m=ml_m,
                      n_folds=3)

dml_irm.fit()

# --- Projetando a Heterogeneidade (CATE) ---
# "Como o efeito causal varia linearmente com as features X?"
cate_res = dml_irm.cate(basis=df[[f'X{i}' for i in range(5)]])

print(cate_res)

Interpretando o CATE: Se no resultado do cate_res o coeficiente de uma variável (ex: X1: Idade) for positivo e significante, indica que o tratamento é mais eficaz quanto maior for a idade do indivíduo.

Relembrando!

PLR: Assume que o efeito do tratamento ( $θ$ ) entra de forma aditiva e linear (não interage complexamente com $X$ na equação estrutural). É ideal para tratamentos contínuos (ex: preço, dosagem).

IRM: É desenhado especificamente para tratamentos binários. Permite interações completas entre o tratamento e as covariáveis, sendo mais robusto para heterogeneidade. Utiliza o estimador AIPW (Augmented Inverse Probability Weighting) por trás dos panos, que possui a propriedade de Dupla Robustez (Doubly Robust).

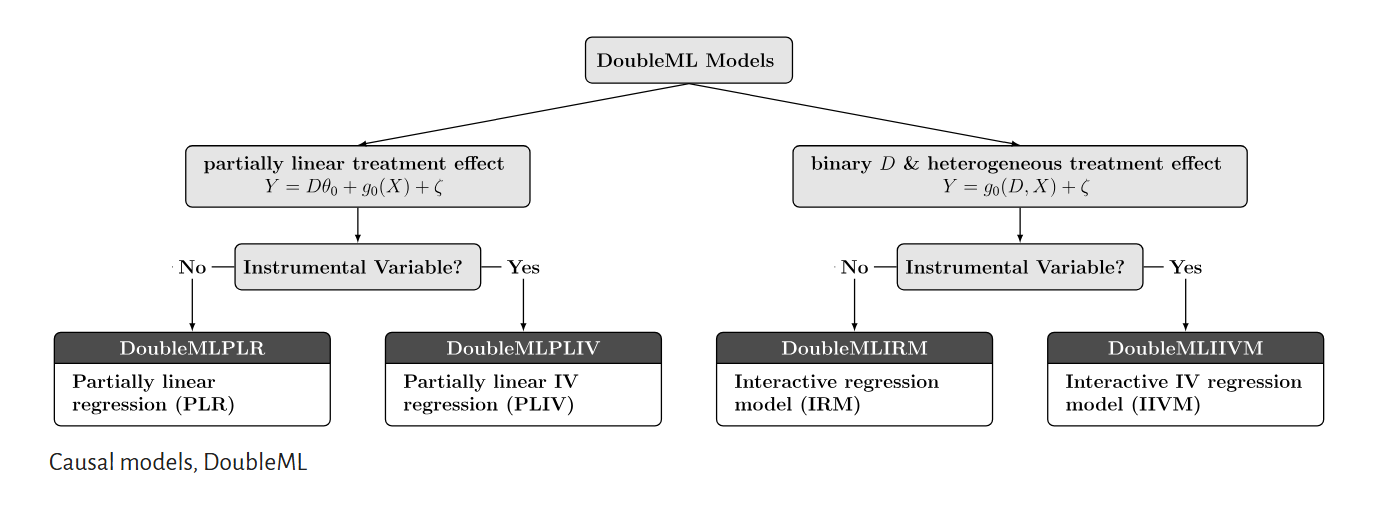
Introduction to Causal Machine Learning with DoubleML for Python

3. Calculando o GATE (Group Average Treatment Effect)

A biblioteca DoubleML oferece um método dedicado .gate(), para efeito médio segmentado por grupo. Para utilizá-lo, precisamos passar um DataFrame onde as colunas representam os grupos (indicadores binários/dummies).

Nota

Podemos calcular o GATE agregando as estimativas do CATE. Filtramos as unidades que pertencem ao grupo de interesse e tiramos a média dos seus efeitos causais estimados ( $\hat{τ} (x)$ ).

# --- Passo 1: Definir os Grupos de Interesse ---
# Vamos criar, por exemplo, dois grupos baseados na variável X1 (ex: Idade normalizada)
# Grupo 0: X1 <= 0.5
# Grupo 1: X1 > 0.5
groups = pd.DataFrame({
    'Grupo_Baixo_X1': df['X1'] <= 0.5,
    'Grupo_Alto_X1':  df['X1'] > 0.5
})

# --- Passo 2: Calcular o GATE via DoubleML ---
# O método gate() ajusta uma regressão linear dos resíduos contra essas variáveis de grupo
gate_res = dml_irm.gate(groups=groups)

print(gate_res)

# --- Passo 3: Analisar os Intervalos de Confiança ---
# Verificamos se o intervalo de 95% cruza o zero ou se os grupos se sobrepõem
print(gate_res.confint())

DoubleML com Variáveis Instrumentais (IV)

Diferente do DoubleML padrão (que limpa $X$ apenas de $Y$ e $D$ ), no cenário com Variável Instrumental nós precisamos limpar a influência das covariáveis ( $X$ ) de três lugares: do Resultado ( $Y$ ), do Tratamento ( $D$ ) e do Instrumento ( $Z$ ).

Simulando o DoubleMLPIV para ter uma ideia, o processo envolve 3 modelos de Machine Learning e uma regressão IV 2SLS final.

Premissas

$Y$ depende de $X, D, U$ .
$D$ depende de $X, Z, U$ .
$Z$ depende de $X$

1. Previsão

Primeiro, usamos ML para prever $Y$ , $D$ e $Z$ usando apenas as covariáveis $X$ . O objetivo é capturar toda a variação explicada por variáveis de confusão.

Modelo 1 ( $q (X)$ ): Prever $Y$ usando $X$ .
Modelo 2 ( $m (X)$ ): Prever $D$ usando $X$ .
Modelo 3 ( $r (X)$ ): Prever $Z$ usando $X$ .

2. Ortogonalização Tripla

Subtraímos as previsões dos valores reais.

$\tilde{Y} = Y - {\hat{Y}}_{M L}$ (Variação no outcome não explicada por $X$ )
$\tilde{D} = D - {\hat{D}}_{M L}$ (Variação no tratamento não explicada por $X$ )
$\tilde{Z} = Z - {\hat{Z}}_{M L}$ (Variação no instrumento não explicada por $X$ )

3. Estágio Final (2SLS nos Resíduos)

Usamos os resíduos do instrumento ( $\tilde{Z}$ ) para instrumentar os resíduos do tratamento ( $\tilde{D}$ ) e explicar os resíduos do resultado ( $\tilde{Y}$ ).

import numpy as np
import pandas as pd
import statsmodels.api as sm
from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier

# --- 1. Gerando Dados Fictícios (Endógenos) ---
np.random.seed(42)
n = 1000
# X afeta tudo (confusão)
X = np.random.normal(0, 1, (n, 3)) 
# Z (instrumento) afeta D, mas também depende de X
Z = 0.5*X[:,0] + np.random.normal(0, 1, n) 
# U (não observado) afeta D e Y
U = np.random.normal(0, 1, n) 
# D (tratamento) depende de X, Z e U (viés)
D = 0.5*Z + 0.5*X[:,0] + U + np.random.normal(0, 0.5, n)
# Y (outcome) depende de D, X e U. Efeito real de D é 2.0
Y = 2.0*D + X[:,0] + U + np.random.normal(0, 0.5, n) 

df = pd.DataFrame({'Y': Y, 'D': D, 'Z': Z})
X_cols = pd.DataFrame(X, columns=['X1', 'X2', 'X3'])

# --- 2. Fase de Machine Learning ---
# Treinamos modelos para capturar a influência de X em Y, D e Z

# a) Prever Y dado X
model_y = RandomForestRegressor(max_depth=5).fit(X_cols, df['Y'])
y_hat = model_y.predict(X_cols)
y_res = df['Y'] - y_hat  # Resíduo Y (Ortogonalizado)

# b) Prever D dado X
model_d = RandomForestRegressor(max_depth=5).fit(X_cols, df['D'])
d_hat = model_d.predict(X_cols)
d_res = df['D'] - d_hat  # Resíduo D (Ortogonalizado)

# c) Prever Z dado X (Essencial para DoubleMLPIV!)
model_z = RandomForestRegressor(max_depth=5).fit(X_cols, df['Z'])
z_hat = model_z.predict(X_cols)
z_res = df['Z'] - z_hat  # Resíduo Z (Ortogonalizado)

# --- 3. 2SLS clássico ---
# y_res ~ beta * d_res (instrumentado por z_res)

# 1º Estágio Manual: Regredir d_res contra z_res
stage1 = sm.OLS(d_res, sm.add_constant(z_res)).fit()
d_res_hat = stage1.predict() # Variação de D limpa de X e induzida por Z limpo

# 2º Estágio Manual: Regredir y_res contra o predito do 1º estágio
stage2 = sm.OLS(y_res, sm.add_constant(d_res_hat)).fit()

Tratamentos Contínuos

Para essas condições, utilizamos o PLR, mas com uma abordagem conceitualmente um pouco diferente, mas ainda podemos utilizar o DoubleML.

1. ATE

Se você quer saber "Qual é a elasticidade média do preço na demanda?", a PLR padrão que vimos antes resolve perfeitamente.

Modelo de Outcome $l (X)$ : Regressão (Random Forest Regressor, XGBoost Regressor).
Modelo de Tratamento $m (X)$ : Regressão (não Classificação!). Aqui estimamos $E [D | X]$ (ex: qual o preço esperado para um produto com essas características).
Final: Regressão linear dos resíduos.

A intuição é: "Depois de remover o efeito das características do produto, se eu subo o preço em R$1 (resíduo), quanto cai a venda (resíduo)?"

2. Efeito Heterogêneo / CATE

E se você quiser saber: "A sensibilidade ao preço muda dependendo da renda do cliente?"

Aqui a equação muda. Não assumimos mais um $θ$ fixo, mas sim uma função $θ (X)$ :

Y = D \cdot θ (X) + g (X) + U

Para resolver isso com DML em tratamentos contínuos, mantemos a estrutura da PLR, mas alteramos a etapa final.

O Processo Adaptado

Ortogonalização:
- Limpamos $Y$ usando ML ( $Y_{r e s} = Y - \hat{E} [Y | X]$ ).
- Limpamos $D$ usando ML ( $D_{r e s} = D - \hat{E} [D | X]$ ).
Estimação do CATE (A Mudança):
- Em vez de fazer OLS(Y_res ~ D_res), nós projetamos a relação sobre as variáveis $X$ .
- Basicamente, rodamos uma regressão onde o coeficiente de $D_{r e s}$ interage com $X$ .

Y_{r e s} \approx θ (X) \cdot D_{r e s}

Exemplo

Imagine que queremos ver a elasticidade-preço ( e como ela varia por renda e idade.

from doubleml import DoubleMLPLR
from sklearn.ensemble import RandomForestRegressor

# Nota: Para tratamento contínuo, AMBOS os modelos devem ser Regressores
ml_l = RandomForestRegressor() # Prever Vendas (Outcome)
ml_m = RandomForestRegressor() # Prever Preço (Tratamento Contínuo)

# 1. Ajustar o PLR
dml_plr = DoubleMLPLR(data_dml,
                      ml_l=ml_l,
                      ml_m=ml_m,
                      n_folds=3)
dml_plr.fit()

# O 'coef' aqui é a elasticidade MÉDIA (ATE)
print(f"Elasticidade Média: {dml_plr.coef}")

# 2. Estimando CATE (Heterogeneidade)
# Queremos saber: A elasticidade depende da Renda (X1)?
# O método cate() faz uma regressão dos resíduos: Y_res ~ alpha + beta_1 * D_res * X1
cate_res = dml_plr.cate(basis=df[['X1']])

print(cate_res)