Design de Experimentos

Na introdução ao seu trabalho The Design of Experiments, Ronald Fisher demonstrou preocupação com a falta de clareza e rigor metodológico em experimentos. Ele notou que a ausência de um design experimental robusto poderia levar a:

• Dificuldade de Interpretação: O leitor e, por vezes, o próprio cientista, poderiam ter interpretações diferentes sobre os resultados, levando a conclusões não suportadas pelos dados ou que poderiam ter ocorrido por acaso (chance), mesmo que a hipótese fosse falsa.
• Carência Estrutural (Design): Falhas lógicas e estruturais tornam o experimento fundamentalmente incorreto, muitas vezes devido a controles inadequados ou à ausência de uma comparação válida.

Experimentos mal projetados resultam em desperdício de recursos (tempo e dinheiro) e em decisões estratégicas equivocadas. Em um cenário de tomada de decisão, é imprescindível sermos cautelosos e rigorosos para manter o controle sobre a inferência.

Fisher propôs um método para trazer facilidade e confiança à experimentação, baseando-se em três pilares:

1. Randomização: Garante que características não observáveis se distribuam igualmente entre os grupos, eliminando viés de seleção.

2. Controle: Isola o efeito do tratamento de fatores externos (ruído).

3. Replicação: Reduz o erro experimental e aumenta a precisão da estimativa.

Por que não utilizar apenas dados observacionais?

A utilização exclusiva de dados históricos ou observacionais para a extração de conclusões de causa e efeito é metodologicamente errada. A mera existência de grandes volumes de dados não supre a necessidade de um desenho experimental rigoroso. Judea Pearl argumenta que os dados, por si só, operam sob a lógica das probabilidades e proporções, sendo "agnósticos" aos mecanismos causais que os geraram, ou seja, eles não explicitam os mecanismos causais neles contidos. Assumir que qualquer dado observacional permite inferir causalidade sem o conhecimento de como o tratamento foi atribuído, de como as características dos grupos se representam ou se as premissas da inferência causal são atendidas, compromete a integridade dos resultados e pode conduzir a conclusões de pesquisa equivocadas.

A inferência causal a partir de bases observacionais, sem o devido controle sobre o mecanismo de atribuição do tratamento ou o cumprimento de premissas explícitas, invalida a robustez das conclusões. O risco reside, por exemplo, na impossibilidade de isolar o efeito do tratamento de causas comuns entre o tratamento e o outcome e vieses inerentes à coleta passiva de dados.

Um exemplo clássico desta limitação é o debate histórico sobre a relação entre o tabagismo e a mortalidade, detalhado no capítulo 05 de The Book of Why. Durante anos, a dependência exclusiva de análises estatísticas e dados observacionais, dada a ausência de um framework causal robusto na época, permitiu que correlações fossem utilizadas para contestar a causalidade direta, retardando intervenções de saúde pública.

Embora métodos quasi-experimentais busquem mitigar tais limitações quando a randomização é inviável, eles ainda dependem de premissas rigorosas de identificação. Sem o controle experimental, a transição da correlação para a causalidade permanece um salto metodológico arriscado.

Experimentos Aleatorizados

Para contornar o Problema Fundamental da Inferência Causal, suprir a carência de design de experimentos e controlar o viés de variável omitida, recorre-se a métodos de pesquisa como o Experimento Aleatorizado.

O experimento aleatorizado, ou ensaio clínico randomizado (RCT), é um procedimento no qual as unidades de uma amostra populacional são alocadas de forma aleatória (randomizada) ao grupo de tratamento ou ao grupo de controle.

A randomização é crucial, pois:

• Elimina vieses de seleção e confusão.
• Cria grupos estatisticamente comparáveis (balanceados).

Ao garantir que a única diferença sistemática esperada entre os grupos seja a aplicação do tratamento, a randomização permite que a diferença observacional nos resultados seja interpretada como uma estimativa válida do efeito causal médio do tratamento na população.

Lecture 3 – The Magic of Randomized Control Trials

Lecture 3 – The Magic of Randomized Control Trials

Premissas

Molak, em conversa com Thanos Vlontzos enfatiza que nunca nos livramos totalmente das premissas. Todo modelo, causal ou não, repousa sobre suposições; o objetivo não é eliminá‑las, mas escolher aquelas com as quais podemos conviver e torná‑las explícitas. Segundo ele, o problema não é ter premissas iniciais, e sim esquecê‑las: uma suposição negligenciada pode fazer um projeto parecer perfeito na superfície, mas esconder uma "mancha enorme" que, mais tarde, causará problemas. Isso vale tanto para estudos experimentais quanto especialmente para estudos observacionais. As premissas que devemos respeitar são:

• SUTVA (Stable Unit Treatment Value Assumption)
  - Consistência: O tratamento é bem definido; o outcome observado para uma unidade sob o tratamento $D$ é igual ao resultado potencial $Y(D)$.
  - Sem interferência: O tratamento de uma unidade não afeta o resultado de outra (sem spillovers/efeitos indiretos).
• Ignorabilidade / Unconfoundedness / Exchangeability
  - Os resultados potenciais são independentes da atribuição do tratamento, condicional às covariáveis observadas: $\{Y(0),Y(1)\}\perp D|X$. Em RCTs ideais, a randomização garante ignorabilidade por definição.
• Positividade / Overlap
  - Para todo valor de $X$ considerado, há probabilidade estritamente positiva de receber cada condição: $0<P(T=1|X)<1$. Sem positividade, não é possível comparar contrafactuais em certas subpopulações.
• Controle de confundidores
  - Em estudos observacionais: Medir e ajustar os confundidores (regressão, propensity scores, IPW, etc.).
  - Em RCTs: Projetar estratificação quando necessário para garantir balanceamento e ajustar para covariáveis na análise para melhorar a precisão (redução de variância).
• Ameaças pós-randomização
  - Não-adesão (noncompliance), perda amostral diferencial (attrition), contaminação e mediadores induzidos pelo tratamento podem reintroduzir viés de seleção.

Pontos de Atenção

• Validade Interna:
  • Definição: Refere-se à confiança de que o efeito observado no resultado é causado unicamente pela manipulação do tratamento (variável independente) e não por fatores externos, vieses ou erros de condução. Um experimento tem alta validade interna se pudermos afirmar com certeza que o tratamento causou a mudança no resultado.
  • Ameaças: Seleção dos participantes, mudanças naturais ao longo do tempo, eventos externos durante o experimento e mortalidade/perda amostral.
• Validação Externa: Trata-se da capacidade de generalizar os resultados do experimento para a população mais ampla ou para outros ambientes e contextos. Se os resultados só se aplicam à amostra específica estudada, a validade externa é baixa.
  • Ameaças: Interação entre seleção e tratamento (o efeito só existe no grupo específico selecionado) e efeitos de laboratório (condições artificiais que não refletem o mundo real).
• Validade de Construto
  • Definição: Refere-se à adequação das medidas. Garante que as variáveis operacionais (como você mede ou manipula algo) realmente representam os construtos teóricos (os conceitos abstratos estudados).
  • Em outras palavras: É a certeza de que o experimento está medindo aquilo que se propôs a medir.
  • Ponto de Atenção:
    • Deve-se garantir que as métricas realmente capturem a essência dos conceitos (ex: satisfação do cliente, motivação).
    • Ameaças Comuns:
      • Sub-representação do Construto: A métrica é incompleta e não captura a totalidade do conceito.
      • Variância de Métodos Irrelevantes: A medição é contaminada por fatores alheios ao conceito de interesse.
• Efeito Spillover (Violação da SUTVA):
  • Ocorre quando o tratamento aplicado ao Grupo de Tratamento afeta, indiretamente, o Grupo de Controle (ou vice-versa). O tratamento "vaza" ou a informação/benefício se espalha.
    • Exemplos:
      • Um participante do controle aprende sobre a nova funcionalidade com um amigo do tratamento.
      • Um participante do grupo de controle aprende sobre a nova funcionalidade com um amigo do grupo de tratamento (contaminação).
      • A mudança de preço em uma loja (tratamento) altera a demanda de uma loja vizinha (controle).
      • Em experimentos geográficos, a intervenção em uma área afeta a área contígua.
    • Implicação: Se houver spillover, o grupo de controle deixa de ser uma linha de base pura, comprometendo a validade interna. A estimativa do efeito será enviesada.
    • Mitigação: Usar clusters/agrupamentos distantes (geográfica ou socialmente) ou implementar cegamento rigoroso.

Análise de Poder Estatístico e Tamanho de Amostra

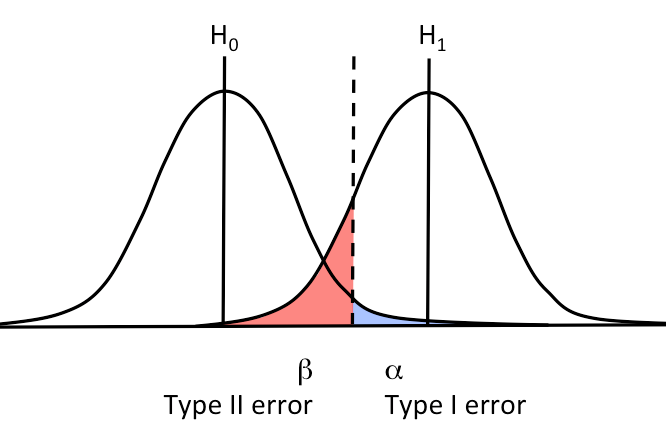
No contexto de estudos experimentais, a inferência continua sendo probabilística. Ao tomarmos uma decisão sobre rejeitar ou não a Hipótese Nula ($H_0$), estamos sujeitos a cometer erros. O "Poder Estatístico" é, fundamentalmente, uma medida de nossa capacidade de evitar um desses erros: o de não ver algo que realmente existe.

A Matriz de Decisão (Erros Tipo I e II)

A melhor forma de visualizar os riscos é através da matriz de decisão. Imagine que existe uma "Verdade Universal" (que não conhecemos) e uma "Decisão do Cientista" (baseada nos dados).

• Erro do Tipo I ($\alpha$ - Falso Positivo): É o risco de afirmar que o tratamento funciona quando ele é inócuo. É controlado pelo Nível de Significância. Ocorre quando rejeitamos a $H_0$ quando ela é, na verdade, verdadeira.

• Erro do Tipo II ($\beta$ - Falso Negativo): É o risco de dizer que "não houve mudança", quando na verdade o tratamento funcionou. Ocorre quando falhamos em rejeitar a $H_0$ quando ela é, na verdade, falsa.

• Poder do Teste ($1-\beta$): É a probabilidade de não cometer o Erro Tipo II. Se o Poder é 80%, significa que, se o tratamento for eficaz, temos 80% de chance de detectá-lo.

Os 4 Pilares da Análise de Poder

A Análise de Poder descreve o equilíbrio matemático entre quatro variáveis interdependentes.

1. Tamanho da Amostra ($n$): A quantidade de unidades no experimento.

   • Relação: Quanto maior o $n$, menor o erro padrão e maior o Poder.

2. Nível de Significância ($\alpha$): O critério de rigor para o "falso positivo".

   • Relação: Ser mais rigoroso (ex: baixar $\alpha$ de 5% para 1%) torna mais difícil rejeitar a nula, o que diminui o Poder (aumenta o risco de Falso Negativo).

3. Tamanho do Efeito / MDE ($\delta$): A magnitude da diferença que queremos detectar.

   • Relação: Efeitos grandes são "fáceis" de ver (ex: um aumento de 50% na conversão). Efeitos minúsculos exigem mais amostra.

4. Poder Estatístico ($1-\beta$): A sensibilidade do teste.

Efeito Mínimo Detectável (MDE)

Se tratando de poder, o MDE representa a menor mudança que a inferência quer detectar. Ele esta atrelado ao fator da decisão da pesquisa em verificar o impacto do tratamento. Em outras palavras, o quanto você quer verificar que o seu desfecho tenha impacto de negócio, por exemplo implementar uma nova campanha de marketing, com a premissa de um aumento de 5% da receita.

Entretanto, há pontos a serem observados:

• MDE e ROI: Se implementar uma nova funcionalidade custa $1 milhão, um aumento de 0.1% na receita pode não pagar o custo. Logo, seu experimento não precisa ter sensibilidade para detectar 0.1%. Você deve configurá-lo para detectar o ponto de breakeven.

• O Perigo do MDE Baixo: Querer detectar efeitos ínfimos exige amostras exponenciais.

• O Perigo do MDE Alto: Se configurar o estudo para detectar apenas aumentos grandes, e seu tratamento gera um ganho sólido realístico mas abaixo disso, seu teste dirá que "não houve diferença significativa" (Erro Tipo II), e você descartará uma boa ideia. Dificilmente sob ótica de mercado, teremos saltos grandes de efeito de uma funcionalidade nova ou novos produtos, por exemplo, como "revolucionário". Esse valor inclusive, vai depender do contexto a ser estudado. Para tal, podemos utilizar como referências trabalhos anteriores, análises observacionais ou pesquisas de mercado para avaliarmos um MDE realístico.

Curva de Poder

A Curva de Poder é uma representação gráfica que mostra como o poder estatístico varia em função do tamanho do efeito real. Ela é interessante para compreender as limitações e capacidades do seu experimento, o que facilita comunicar entre as partes em relação a pesquisa. Para bom entendimento, sugiro a leitura recomendada.

Para fins didáticos, implementei algumas funções para análise de poder e verificar o MDE. Aconselho não apenas veja os resultados do jupyter notebook, mas as funções criadas na minha biblioteca.

Elementos fundamentais do desenho experimental

Para responder a uma pergunta de pesquisa com objetivo causal, é imperativo definirmos, de forma mensurável, os componentes estruturais do estudo. Esta ausência torna a inferência sujeita a interpretações contraditórias.

1. Tratamento ($D_i$)

Refere-se à intervenção ou exposição que está sendo investigada.

• Definição Operacional: Descreva exatamente o que constitui "receber o tratamento". Evite ambiguidades. Por exemplo, em vez de "receber um cupom", especifique "receber um cupom de 10% de desconto via e-mail às 09:00".

• Escopo e Intensidade: O tratamento é binário ($D\in \{0,1\}$), contínuo (ex: dose de um medicamento) ou multivalorado (ex: variações A/B/C)?

• Consistência e SUTVA: A definição deve ser clara o suficiente para garantir que não existam múltiplas versões ocultas do tratamento que afetem o resultado de formas diferentes, violando SUTVA. Se duas pessoas recebem $D_i=1$, elas devem ter recebido essencialmente a mesma intervenção.

2. Potenciais Outcomes ($Y_i(0),Y_i(1)$)

Os potenciais outcomes representam os resultados teóricos que a unidade $i$ apresentaria sob cada condição de tratamento.

• Mensurabilidade: Como o outcome observado $Y_i$ será coletado? Temos dados confiáveis para mensurar o estado contrafactual, seja via desenho experimental (RCT) ou métodos observacionais?

• Definição da Métrica: Especifique a métrica exata e a janela temporal.

  • Exemplo: "Conversão" é vago. "Compra confirmada ($Y>0$) no período de 7 dias após a exposição" é preciso.

  • Transformações: Defina previamente se usará a métrica bruta, logaritmo, ou taxas.

• Validade de Construto: A métrica escolhida realmente representa o conceito que queremos estudar? Uma definição robusta minimiza o erro de medição e garante que estamos capturando o fenômeno de interesse.

3. Unidade de Observação ($U_i$)

Define a entidade fundamental sobre a qual o tratamento é aplicado e o desfecho é medido.

• Nível de Agregação: Quem é a unidade experimental? Um usuário individual, uma sessão de navegador, uma loja física ou um município?

• Alinhamento Tratamento-Unidade: É crucial verificar se a unidade de análise coincide com a unidade de randomização/tratamento.

• Interferência: A escolha da unidade afeta a probabilidade de interferência entre unidades? É preciso observar para não violar a SUTVA.

• Validade Externa: As características das unidades observadas na amostra permitem generalizar os resultados para a população-alvo?

4. Estimand (O parâmetro de interesse)

O Estimand é a quantidade teórica exata que queremos estimar. Ele guia todo o desenho do estudo e o cálculo do tamanho da amostra.

• Definição do Parâmetro: O que queremos descobrir?

  • ATE (Average Treatment Effect): O efeito médio para toda a população. $\mathbb{E}[Y(1)-Y(0)]$.

  • ATT (Average Treatment Effect on the Treated): O efeito médio apenas para quem de fato recebeu o tratamento.

  • CATE (Conditional Average Treatment Effect): O efeito médio para um subgrupo específico (heterogeneidade).

Mecanismo de Atribuição

O mecanismo de atribuição é o processo (conhecido ou desconhecido) que determina quais unidades recebem o tratamento e quais recebem o controle. Formalmente, ele descreve a lei de probabilidade condicional $P(W|X,Y(0),Y(1))$ que governa a alocação do tratamento $W$.

Em um RCT, este mecanismo é controlado e conhecido (ex: moeda, sorteio). Em estudos observacionais, ele é desconhecido e precisa ser estimado. Essa estimativa é justamente o cálculo da probabilidade de receber o tratamento $P(W=1|X)$, valor que chamamos de Escore de Propensão, ao qual nos permite rebalancear os grupos e validar se as premissas de identificação foram respeitadas.

Em outras palavras, quanto mais conhecermos sobre o seus dados e o mecanismo de atribuição, melhor e verdadeira serão suas estimativas. Dentro do contexto causal, não podemos atuar de olhos fechados. Necessitamos conhecer a fundo tudo o que contempla o design de experimento, para aí sim, irmos para algum estudo e inferência.

Problemas com Experimentos Aleatorizados

Em um RCT, os participantes são distribuídos aleatoriamente para o grupo de tratamento ou controle. Essa randomização visa equilibrar todas as variáveis de confusão (tanto as conhecidas quanto as desconhecidas) entre os grupos, permitindo que qualquer diferença observada no resultado seja atribuída, com alta confiança, à intervenção (causa).

Embora seja o padrão de ouro na metodologia experimental, ele não oferece uma garantia absoluta de causalidade, pois a randomização inicial é apenas o primeiro passo. A causalidade pode ser comprometida por vieses pós-randomização que surgem durante a execução do estudo. Problemas como a desigualdade de características entre os participantes, perda ou até abandono podem prejudicar o resultado para uma generalização dos resultados.

Além das limitações metodológicas na condução do estudo, o RCT é inviável ou antiético em inúmeros cenários de pesquisa causal. Existem fenômenos de interesse (como o efeito de eventos raros, exposições de longuíssimo prazo, ou variáveis não manipuláveis, como o status socioeconômico) onde a aleatoriedade é inatingível. Mais gravemente, a randomização é antiética em exposições que são sabidamente prejudiciais. Por exemplo, seria moralmente inaceitável randomizar uma população para forçar um grupo a fumar a fim de analisar as chances de câncer de pulmão.

Portanto, em contextos onde a intervenção não pode ser controlada por um RCT devido a impedimentos éticos ou práticos, os pesquisadores devem recorrer a outras ferramentas, como também é possível aplicar outros tipos de amostragens.